ŦPķiūĮēßĩûĶôļę·―ŪwĒwšôĪWūĮŧPąÐĪäīĐ
ŽÛÃöŠšūĮŽėŠūÃŅ (KS1-S2-2)
ĶbĨŧūĮēßģæĶėĪĪĄAūĮĨÍĨuŧÝĨΊ―Æ[ŠšĪčŠkŋëŧ{Š―ĻĪĄBĩĨļyĐMĩĨÃäĪTĻĪ§ÎŦKĨiĄAĨHĪU§ũŪÆķČĻŅąÐŪv§@ūĮŽėŠūÃŅŠš°ŅĶŌĄAĩLŧÝĨΧ@ąÐūĮŠšĪšŪeĄG
ĄP ĩĨÃäĪTĻĪ§ÎŽOĩĨļyĪTĻĪ§Î
ĄP
ĩĨÃäĪTĻĪ§ÎÄÝĩĨļyĪTĻĪ§ÎĪ§ĶCĄC
(ĪEģđĨXŠĐŠĀ―sŋčģĄ(1995)ĄCĄmĪĪūĮžÆūĮÃãĻåĄnĄCĨxĨ_ĄGĪEģđĨXŠĐŠĀĄCķ204ĄC)
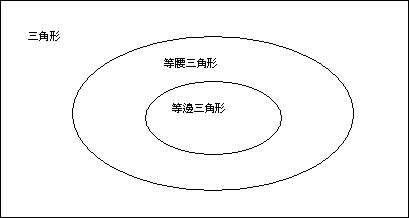
ĄP
ĩĨļyĪTĻĪ§ÎŠš§PĐwĄGĶpŠGĪ@ÓĪTĻĪ§ÎĶģĻâÓĻĪŽÛĩĨĄAĻšŧōĻâÓĻĪĐŌđÃäĪ]ŽÛĩĨĄAģoÓĪTĻĪ§ÎīNŽOĩĨļyĪTĻĪ§ÎĄC
(Ĩ_ĻĘŪv―dūĮ°|žÆūĮĻtĄmĪĪūĮžÆūĮÃãĻåĄn―sžgēÕ(1987)ĄCĄmĪĪūĮžÆūĮÃãĻåĄnĄCŦnĐũĨŦĄGĶŋĶčąÐĻ|ĨXŠĐŠĀĄCķ214ĄC)
ĄP
ĩĨÃäĪTĻĪ§ÎÄÝĩĨļyĪTĻĪ§ÎĪ§ĶCĄC
(ĪEģđĨXŠĐŠĀ―sŋčģĄ(1995)ĄCĄmĪĪūĮžÆūĮÃãĻåĄnĄCĨxĨ_ĄGĪEģđĨXŠĐŠĀĄCķ204ĄC)
ĄP
Isosceles ĄGhaving
two sides of equal length, and the angles opposite those sides equal.
(Borrowski,E.J.
& Borwein, J.M.(1989) Dictionary of mathematics. London:Collins)
ĄP
An isosceles triangle is usually defined
as a triangle with at least two sides congruent. Because of this an equilateral
triangle is considered to be a special type of isosceles triangle.
(OĄĶDaffer, P.G. & Clemens, S.R. (1992) Geometry: an investigative approach. Reading, Mass: Addison- Wesley.)